Flambagem e a Regra da Secante

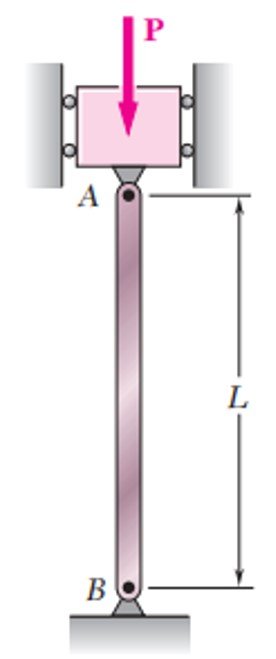
A Figura 1 mostra uma coluna esbelta biarticulada sob o efeito de um carregamento P centrado e paralelo ao eixo vertical. Sabemos que a coluna não se flambará se a intensidade de P não exceder um valor crítico P_cr definido pela seguinte equação:

$\displaystyle {{P}_{{cr}}}=\frac{{{{\pi }^{2}}EI}}{{{{L}^{2}}}}\,\,\,(1)$

onde E é o módulo de elasticidade, I é o momento de inércia da seção transversal com relação ao eixo mais fraco e L é o comprimento da coluna. Como, para propósitos de dimensionamento, é mais comum falarmos em termos de esforços do que forças, podemos utilizar I = Ar², onde r é o raio de giração e A é a área de seção transversal; substituindo e ajustando, temos:

$\displaystyle {{P}_{{cr}}}=\frac{{{{\pi }^{2}}E\times A{{r}^{2}}}}{{{{L}^{2}}}}$

$\displaystyle \therefore \frac{{{{P}_{{cr}}}}}{A}=\frac{{{{\pi }^{2}}E{{r}^{2}}}}{{{{L}^{2}}}}$

$\displaystyle \therefore \frac{{{{P}_{{cr}}}}}{A}=\frac{{{{\pi }^{2}}E}}{{{{{\left( {{L}/{r}\;} \right)}}^{2}}}}$

$\displaystyle \therefore {{\sigma }_{{cr}}}=\frac{{{{\pi }^{2}}E}}{{{{{\left( {{L}/{r}\;} \right)}}^{2}}}}\,\,\,(2)$

Onde $\displaystyle {{\sigma }_{{cr}}}$ é a tensão crítica abaixo da qual a coluna não flambará. Nessa relação, L/r é o índice de esbeltez da coluna, que, como sugere o nome, age como uma medida da flexibilidade da estrutura. É importante frisar que a análise acima somente será válida se $\displaystyle {{\sigma }_{{cr}}}$ for menor que o limite proporcional $\displaystyle {{\sigma }_{Y}}$ do material que constitui a coluna.

Figura 1. Coluna biarticulada sob carregamento axial centrado.

A abordagem euleriana das equações (1) e (2) pressupõe que o carregamento P imposto sobre a coluna é dirigido ao longo do centroide da sua seção transversal e, ademais, que a coluna é perfeitamente reta. Essas são hipóteses pouco realistas, já que carregamentos dificilmente são livres de excentricidade e colunas raramente são perfeitamente retas.

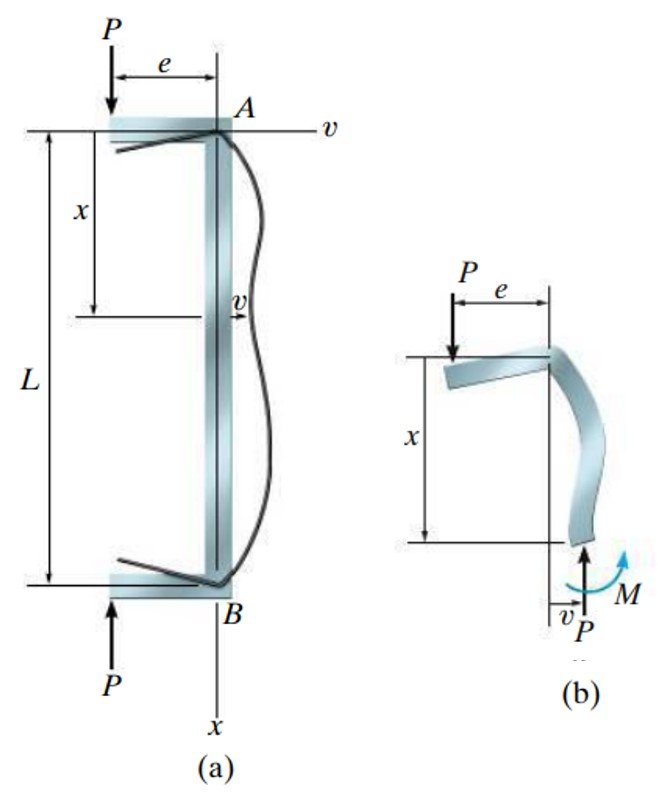
Felizmente, não é difícil incorporar a excentricidade de um carregamento em uma análise de flambagem. Para tanto, considere a coluna esboçada na Figura 2a. A coluna, de comprimento L, está sob o efeito de um carregamento P que tem excentricidade e com relação ao centroide da seção transversal. A excentricidade do referido carregamento produz um momento fletor de intensidade M, o qual, como mostra o diagrama de corpo livre da Figura 2b, é tal que:

$\displaystyle M=-P\left( {v+e} \right)\,\,\,(3)$

onde v é a deflexão lateral. Lembramos agora que a deflexão v relaciona-se ao momento M pela expressão

$\displaystyle \frac{{{{d}^{2}}v}}{{d{{x}^{2}}}}=\frac{M}{{EI}}\,\,\,(4)$

de modo que, substituindo M pela equação (3) e ajustando, temos

$\displaystyle \frac{{{{d}^{2}}v}}{{d{{x}^{2}}}}=-\frac{P}{{EI}}\left( {v+e} \right)$

$\displaystyle \therefore \frac{{{{d}^{2}}v}}{{d{{x}^{2}}}}=-\frac{P}{{EI}}v-\frac{{Pe}}{{EI}}$

$\displaystyle \therefore \frac{{{{d}^{2}}v}}{{d{{x}^{2}}}}+\frac{P}{{EI}}v=-\frac{{Pe}}{{EI}}\,\,\,(5)$

Esta é uma equação diferencial ordinária de segunda ordem cuja solução geral é:

$\displaystyle v={{C}_{1}}\sin \left( {\sqrt{{\frac{P}{{EI}}}}x} \right)+{{C}_{2}}\cos \left( {\sqrt{{\frac{P}{{EI}}}}x} \right)-e\,\,\,(6)$

Figura 2. Coluna sob carregamento excêntrico.

As constantes C₁ e C₂ podem ser obtidas a partir das condições de contorno v(–L/2) = 0 e v(L/2) = 0 (as quais simplesmente dizem que as deflexões nas extremidades da coluna devem ser nulas):

$\displaystyle v\left( {{{-L}}/{2}\;} \right)=-{{C}_{1}}\sin \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)+{{C}_{2}}\cos \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)-e=0\,\,\,(7.1)$

$\displaystyle v\left( {{{+L}}/{2}\;} \right)={{C}_{1}}\sin \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)+{{C}_{2}}\cos \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)-e=0\,\,\,(7.2)$

Resolvendo o sistema de duas equações lineares e duas variáveis, obtemos:

$\displaystyle {{C}_{1}}=0\,\,\,;\,\,\,{{C}_{2}}=e\sec \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)\,\,\,(8)$

Substituindo C₁ e C₂ em (6) e manipulando, temos a seguinte solução para a linha elástica:

$\displaystyle v\left( x \right)={{C}_{1}}\sin \left( {\sqrt{{\frac{P}{{EI}}}}x} \right)+{{C}_{2}}\cos \left( {\sqrt{{\frac{P}{{EI}}}}x} \right)-e$

$\displaystyle \therefore v\left( x \right)=0\times \sin \left( {\sqrt{{\frac{P}{{EI}}}}x} \right)+e\sec \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)\times \cos \left( {\sqrt{{\frac{P}{{EI}}}}x} \right)-e$

$\displaystyle \therefore v\left( x \right)=e\sec \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)\cos \left( {\sqrt{{\frac{P}{{EI}}}}x} \right)-e$

$\displaystyle \therefore v\left( x \right)=e\left[ {\sec \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)\cos \left( {\sqrt{{\frac{P}{{EI}}}}x} \right)-1} \right]\,\,\,(9)$

A deflexão máxima ocorre em x = 0:

$\displaystyle {{v}_{{\max }}}=v\left( {x=0} \right)=e\left[ {\sec \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)\cos \left( {\sqrt{{\frac{P}{{EI}}}}\times 0} \right)-1} \right]$

$\displaystyle \therefore {{v}_{{\max }}}=e\left[ {\sec \left( {\sqrt{{\frac{{P{{L}^{2}}}}{{4EI}}}}} \right)-1} \right]\,\,\,(10)$

Usando I = Ar² e manipulando, obtemos:

$\displaystyle {{v}_{{\max }}}=e\left[ {\sec \left( {\frac{L}{{2r}}\sqrt{{\frac{P}{{EA}}}}} \right)-1} \right]\,\,\,(11)$

Observe que, se e tende a zero, então v_max também tende a zero. No entanto, se o termo em colchetes tende ao infinito enquanto e tende a zero, podemos inferir que nesse caso v_max terá um valor finito e não-nulo. Matematicamente, isso representa o comportamento de uma coluna axialmente carregada que falha quando submetida a um carregamento crítico P_cr. Lembrando que sec x $\displaystyle \to$ $\displaystyle \infty$ quando x = $\displaystyle \pi$ /2, temos:

$\displaystyle \sec \left( {\sqrt{{\frac{{{{P}_{{cr}}}}}{{EI}}}}\frac{L}{2}} \right)=\infty \to \sqrt{{\frac{{{{P}_{{cr}}}}}{{EI}}}}\frac{L}{2}=\frac{\pi }{2}$

$\displaystyle \therefore \sqrt{{\frac{{{{P}_{{cr}}}}}{{EI}}}}L=\pi$

$\displaystyle \therefore \frac{{{{P}_{{cr}}}}}{{EI}}{{L}^{2}}={{\pi }^{2}}$

$\displaystyle \therefore {{P}_{{cr}}}=\frac{{{{\pi }^{2}}EI}}{{{{L}^{2}}}}\,\,\,(12)$

Este resultado é idêntico à fórmula de Euler (equação (1)), como esperaríamos. Convém observar que a equação (11) pode ser reescrita de modo que inclua o carregamento crítico:

$\displaystyle {{v}_{{\max }}}=e\left[ {\sec \left( {\frac{\pi }{2}\sqrt{{\frac{P}{{{{P}_{{\text{cr}}}}}}}}} \right)-1} \right]\,\,\,(13)$

O momento fletor máximo ocorre no ponto médio do comprimento da coluna e tem magnitude dada por M_max = P(v_max + e). Portanto, a tensão máxima na coluna tem intensidade

$\displaystyle {{\sigma }_{{\max }}}=\frac{P}{A}+\frac{{{{M}_{{\max }}}c}}{I}=\frac{P}{A}+\frac{{P\left( {{{v}_{{\max }}}+e} \right)c}}{{A{{r}^{2}}}}\,\,\,(14)$

onde c é a distância do eixo centroidal até a fibra de compressão mais externa. Substituindo v_max, que obtemos pela equação (11), o resultado final é:

$\displaystyle {{\sigma }_{{\max }}}=\frac{P}{A}\left[ {1+\frac{{ec}}{{{{r}^{2}}}}\sec \left( {\frac{L}{{2r}}\sqrt{{\frac{P}{{EA}}}}} \right)} \right]\,\,\,(15)$

Essa importante equação é conhecida como fórmula da secante. A razão ec/r² é denominada razão de excentricidade e o ângulo (L/2r)(P/EA)^1/2 é denominado ângulo de Euler. Embora tenhamos chegado a essa relação por meio da análise de uma coluna biarticulada, outros tipos de coluna podem ser analisados se substituirmos L pelo comprimento efetivo L_e. Podemos reescrever (15) em uma forma que inclui o carregamento crítico P_cr:

$\displaystyle {{\sigma }_{{\max }}}=\frac{P}{A}\left[ {1+\frac{{ec}}{{{{r}^{2}}}}\sec \left( {\frac{\pi }{2}\sqrt{{\frac{P}{{{{P}_{{\text{cr}}}}}}}}} \right)} \right]\,\,\,(16)$

Em uma aplicação típica, possuímos as propriedades do material, as dimensões da coluna e a excentricidade e do carregamento. Isso deixa-nos com duas variáveis na fórmula da secante, quais sejam, a força P e a tensão $\displaystyle {{\sigma }_{{\max }}}$ . Se conhecemos apenas o carregamento P, basta substituí-lo no lado direito de (16), juntamente com as demais variáveis, e com isso determinar $\displaystyle {{\sigma }_{{\max }}}$ . 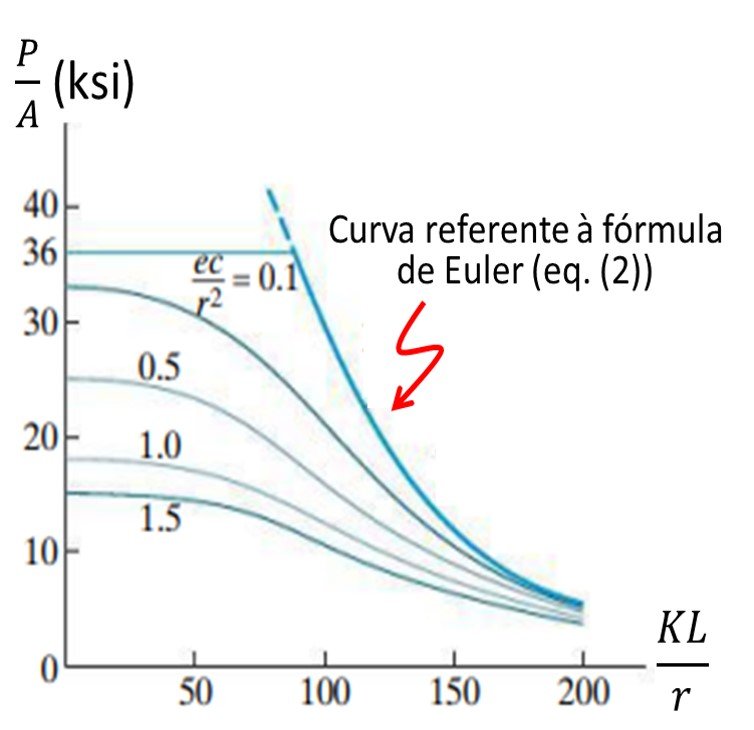Se, por outro lado, conhecemos apenas $\displaystyle {{\sigma }_{{\max }}}$ , as coisas ficam um pouco mais complicadas, pois não existem métodos analíticos para resolver o lado direito de (16) para a variável P; isto é, obtemos uma equação transcendental. No passado, o modo de proceder em tais casos era recorrer a tentativa e erro ou utilizar diagramas de projeto que engenheiros produziam para determinadas combinações de esbeltez, razão de excentricidade e carregamento; um exemplo de diagrama é mostrado na Figura 3. Tais métodos tornaram-se obsoletos com o advento dos computadores, uma vez que softwares como MATLAB (com seus comandos fsolve ou fzero) ou Mathematica (com seus comandos Solve ou FindRoot) podem produzir soluções numéricas para a equação (16) prontamente. Segue que a maior desvantagem da fórmula da secante não é o seu caráter transcendental, mas a determinação prática da excentricidade do carregamento de interesse (Beer e Johnston, 2008; Hibbeler, 2014).

Figura 3. Exemplo de diagrama de dimensionamento para colunas sob carregamento excêntrico. A curva em destaque representa uma coluna sob carregamento centrado.

Exemplo 1

Uma carga axial P é aplicada a uma haste cilíndrica AB de 32 mm de diâmetro, como mostra a figura abaixo. Sendo P = 37 kN e e = 1.2 mm, determine (a) a deflexão no ponto médio C da haste, e (b) A tensão máxima na haste.

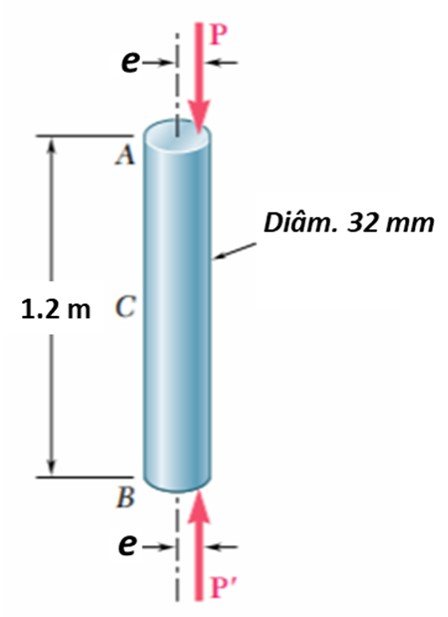
Solução – Parte a. A fibra mais externa é c = d/2 = 32/2 = 16 mm, e o momento de inércia pertinente é:

$\displaystyle I=\frac{\pi }{4}{{c}^{4}}=\frac{\pi }{4}\times {{\left( {16\times {{{10}}^{{-3}}}} \right)}^{4}}=5.15\times {{10}^{{-8}}}\,{{\text{m}}^{4}}$

Em seguida, calculamos o carregamento crítico P_cr:

$\displaystyle {{P}_{{\text{cr}}}}=\frac{{{{\pi }^{2}}EI}}{{{{L}^{2}}}}=\frac{{{{\pi }^{2}}\times \left( {200\times {{{10}}^{9}}} \right)\times \left( {5.15\times {{{10}}^{{-8}}}} \right)}}{{{{{1.2}}^{2}}}}=70.6\,\text{kN}$

A deflexão máxima é dada pela equação (13):

$\displaystyle {{v}_{{\max }}}=0.0012\times \left[ {\sec \left( {\frac{\pi }{2}\sqrt{{\frac{{37}}{{70.6}}}}} \right)-1} \right]=1.66\,\text{mm}\leftarrow$

Parte b. A área de seção transversal A é:

$\displaystyle A=\frac{{\pi \times {{{0.032}}^{2}}}}{4}=8.04\times {{10}^{{-4}}}\,{{\text{m}}^{2}}$

O raio de giração é:

$\displaystyle r=\sqrt{{\frac{I}{A}}}=\sqrt{{\frac{{5.15\times {{{10}}^{{-8}}}}}{{8.04\times {{{10}}^{{-4}}}}}}}=0.008\,\text{m}$

Por fim, a tensão máxima $\displaystyle {{\sigma }_{{\max }}}$ é tal que:

$\displaystyle {{\sigma }_{{\max }}}=\frac{P}{A}\left[ {1+\frac{{ec}}{{{{r}^{2}}}}\sec \left( {\frac{\pi }{2}\sqrt{{\frac{P}{{{{P}_{{\text{cr}}}}}}}}} \right)} \right]=\frac{{37,000}}{{8.04\times {{{10}}^{{-4}}}}}\times \left[ {1+\frac{{0.0012\times 0.016}}{{{{{0.008}}^{2}}}}\sec \left( {\frac{\pi }{2}\times \sqrt{{\frac{{37}}{{70.6}}}}} \right)} \right]$

$\displaystyle {{\sigma }_{{\max }}}=78.9\,\text{MPa}\leftarrow$

Exemplo 2

Uma haste de alumínio (E = 72 GPa) está fixa na base e livre no topo. Se o comprimento da haste é L = 2 m, determine o maior carregamento P que pode ser aplicado à haste sem que esta exceda o limite proporcional $\displaystyle {{\sigma }_{Y}}$ = 410 MPa.

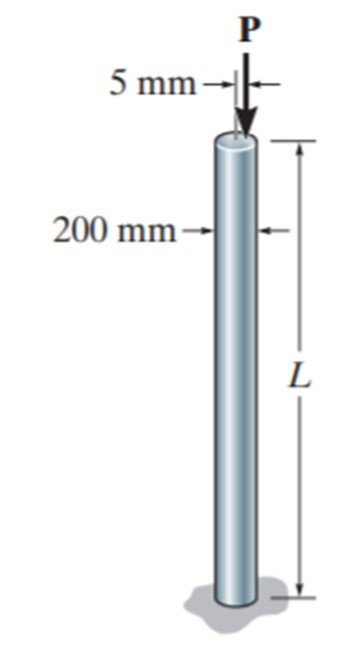
A área da seção transversal da coluna é:

$\displaystyle A=\frac{{\pi \times {{{0.2}}^{2}}}}{4}=0.0314\,{{\text{m}}^{2}}$

O momento de inércia pertinente é:

$\displaystyle I=\frac{\pi }{4}{{c}^{4}}=\frac{\pi }{4}\times {{0.1}^{4}}=7.85\times {{10}^{{-5}}}\,{{\text{m}}^{4}}$

Em seguida, calculamos o raio de giração:

$\displaystyle r=\sqrt{{\frac{I}{A}}}=\sqrt{{\frac{{7.85\times {{{10}}^{{-5}}}}}{{0.0314}}}}=0.05\,\text{m}$

Pela fórmula da secante, a tensão máxima é dada por

$\displaystyle {{\sigma }_{{\max }}}=\frac{P}{A}\left[ {1+\frac{{ec}}{{{{r}^{2}}}}\sec \left( {\frac{{{{L}_{e}}}}{{2r}}\sqrt{{\frac{P}{{EA}}}}} \right)} \right]$

onde o comprimento efetivo L_e para uma coluna engastada em uma extremidade é L_e = 2L, isto é, L_e = 2 $\displaystyle \times$ 2 = 4 m. Fazendo $\displaystyle {{\sigma }_{{\max }}}$ = $\displaystyle {{\sigma }_{Y}}$ = 410 MPa e substituindo acima, temos:

$\displaystyle \frac{{ec}}{{{{r}^{2}}}}=\frac{{0.005\times 0.1}}{{{{{0.05}}^{2}}}}=0.2$

$\displaystyle \frac{{{{L}_{e}}}}{{2r}}\sqrt{{\frac{P}{{EA}}}}=\frac{4}{{2\times 0.05}}\times \sqrt{{\frac{P}{{\left( {72\times {{{10}}^{9}}} \right)\times 0.0314}}}}=8.41\times {{10}^{{-4}}}\sqrt{P}$

$\displaystyle 410\times {{10}^{6}}=\frac{P}{{0.0314}}\times \left[ {1+0.2\sec \left( {8.41\times {{{10}}^{{-4}}}\sqrt{P}} \right)} \right]$

Resta resolver a equação acima para o carregamento P. Podemos utilizar o comando FindRoot no Mathematica:

A solução é P_max = 3.20 $\displaystyle \times$ 10⁶ = 3.20 MN. (Note que Mathematica retorna a raiz mais próxima do valor inicial, e nesse caso escolhi P = 200. Esse valor foi escolhido com base no gráfico da função referente à equação que estamos tentando resolver, o qual pode ser facilmente obtido por meio do comando Plot.)

Para determinar a deflexão máxima, substituímos P_max = 3.20 MN e outras variáveis pertinentes em (13):

$\displaystyle {{v}_{{\max }}}=e\left[ {\sec \left( {\frac{{{{L}_{e}}}}{{2r}}\sqrt{{\frac{P}{{EA}}}}} \right)-1} \right]$

$\displaystyle \therefore {{v}_{{\max }}}=0.005\times \left[ {\sec \left( {\frac{{2\times 2}}{{2\times 0.05}}\sqrt{{\frac{{\left( {3.20\times {{{10}}^{6}}} \right)}}{{\left( {72\times {{{10}}^{9}}} \right)\times 0.0314}}}}} \right)-1} \right]$

$\displaystyle {{v}_{{\max }}}=70.9\,\text{mm}\leftarrow$

Referências

BEER, F.P., JOHNSTON, E.R. Jr., DEWOLF, J.T. e MAZUREK, D.F. (2008). Mecânica dos Materiais. 5ª edição. Nova York: McGraw-Hill.
HIBBELER, R.C. (2014). Mechanics of Materials. 9ª edição. Upper Saddle River: Pearson Prentice-Hall.
SUBRAMANIAN, R. (2010). Strength of Máterials. 2ª edição. Oxford: Oxford University Press.